22nd Graph Drawing Contest
Contest Results
The 22nd Annual Graph Drawing Contest was held in conjunction with the 23rd International Symposium on Graph Drawing and network Visualization (GD 2015).
The contest had two parts: the Creative Topics and the Live Challenge.
The creative topics were provided several months before the conference and focussed on free-form visualisation of specific graphs. Two graphs were provided, and participants were invited to submit any drawings of one or both of the graphs. The submissions were judged by the contest committee during the symposium. This year's topics were a graph of graph classes, and the Tic-Tac-Toe game graph.
The live challenge was held during the conference in a format similar to a typical programming contest, where teams were presented with a collection of challenge graphs and had one hour to submit their highest scoring drawings. This year the challenge focussed on minimizing the crossing number in book embeddings. For details, see here.
Creative Topics: Graph Classes
We received six very nice submissions for this category. We will first list those that unfortunately did not make it to the top three.
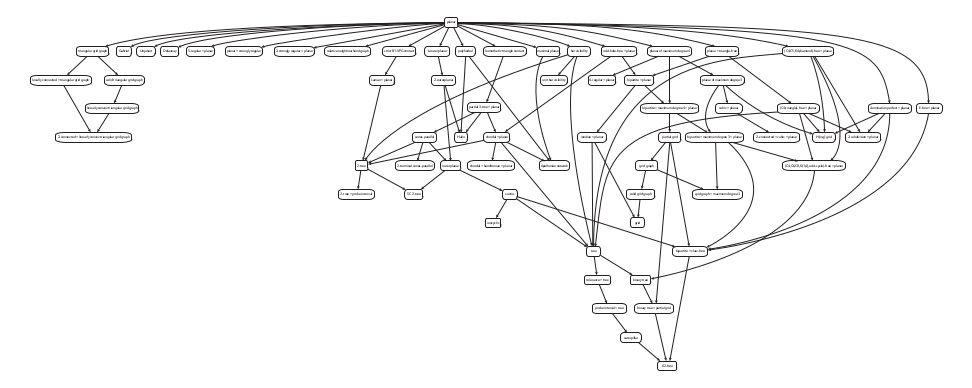
Xiaodong Chen (University of Sydney)
|
Zhang Yu
|
Kaiwen Liang (University of Sydney)
|
Then, we present two runners-up. These drawings were selected for the top three and displayed on large poster boards at the symposium.
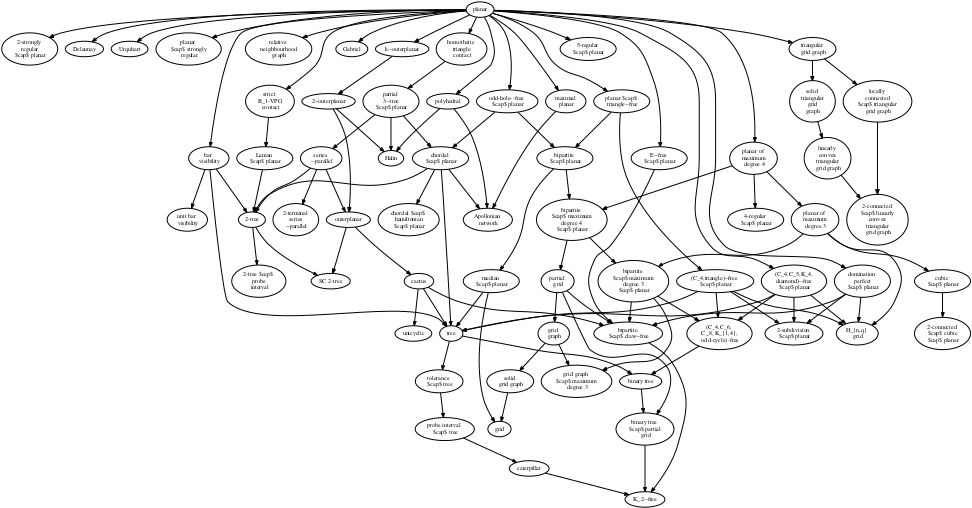
Evmorfia Argyriou, Michael Baur, Anne Eberle, and Martin Siebenhaller (yWorks)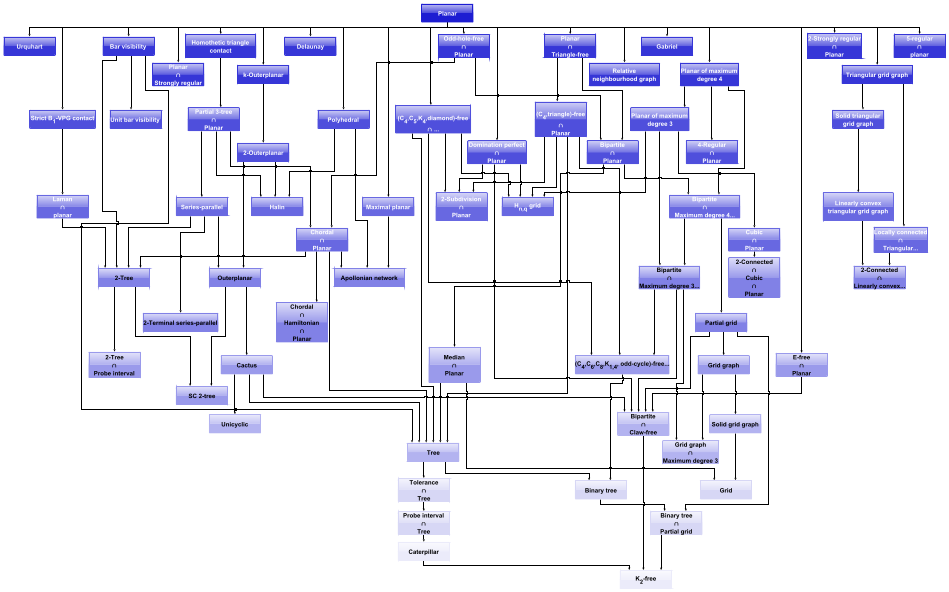
The committee liked the use of edge grouping for nodes with many outgoing edges (such as the "planar" node and the use of visual bridges to reduce the visual ambiguity at crossings. Also, the drawing makes good use of the available space and uses colour as an additional cue to encode distance from the root.
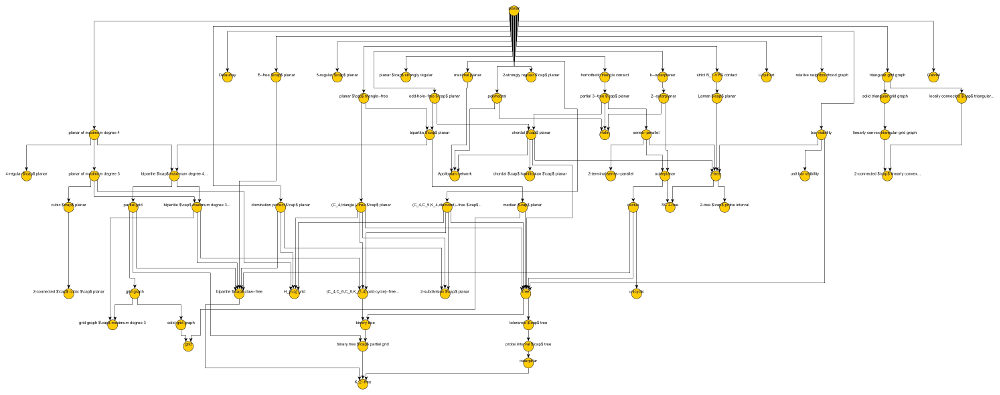
Megah Fadhillah (University of Sydney)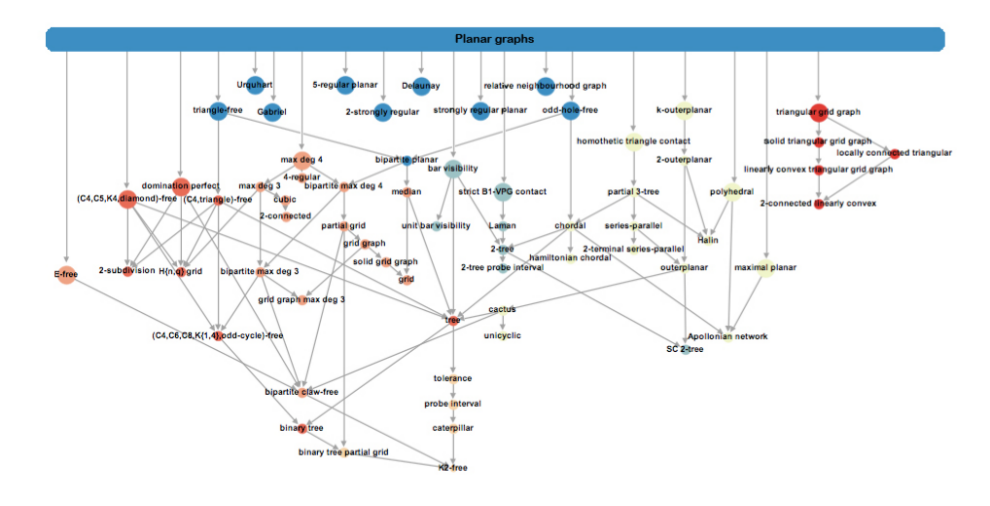
The committee really liked the idea of having a large "planar" node at the top, which acts as a title for the drawing and immediately explains what is being shown. The drawing uses colour to show clusters of nodes and size to encode distance from the root.
Finally, we announce the winner of the 2015 Graph Drawing Contest, Creative Topics: Graph Classes:
TamaraMchedlidze (Karlsruhe Institute of Technology)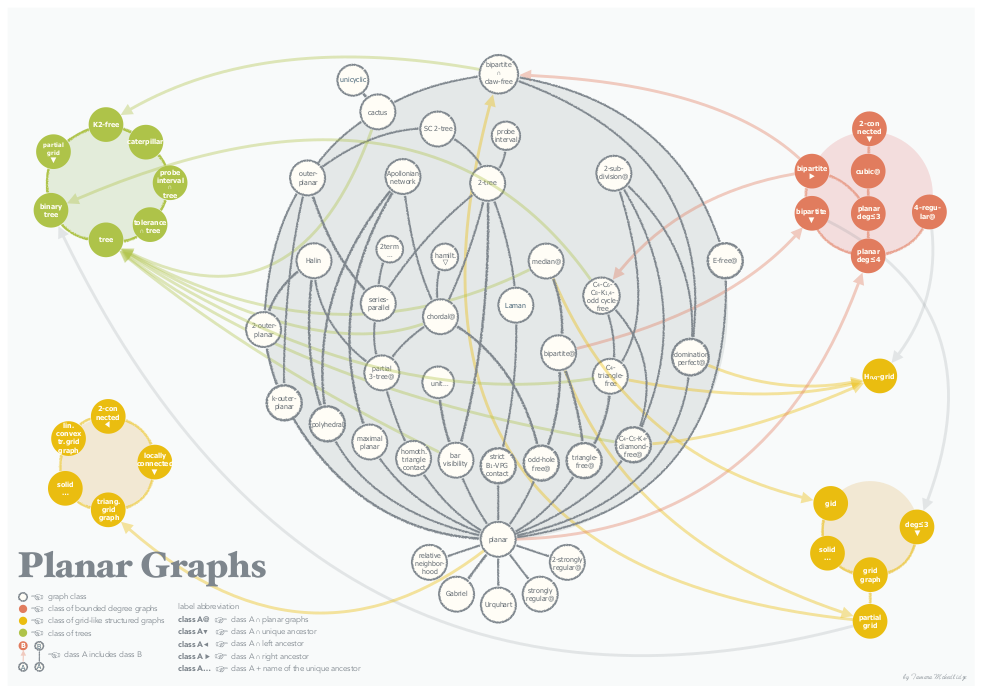
The committee likes the visual appeal of the drawing. The use of circular arcs for edges makes it easy to follow each individual edge, even when they pass behind vertices (something which is traditionally considered bad practice in graph drawing). The drawing uses colour to single out three meaningful groups of nodes: tree classes, bounded degree classes, and grid-like classes. The author also put a lot of thought into abbreviating node labels to increase the readability of the final drawing.
Creative Topics: Tic-Tac-Toe
We received seven very nice submissions for this category. We will first list those that unfortunately did not make it to the top three.
Stephen McCloskey (University of Sydney)
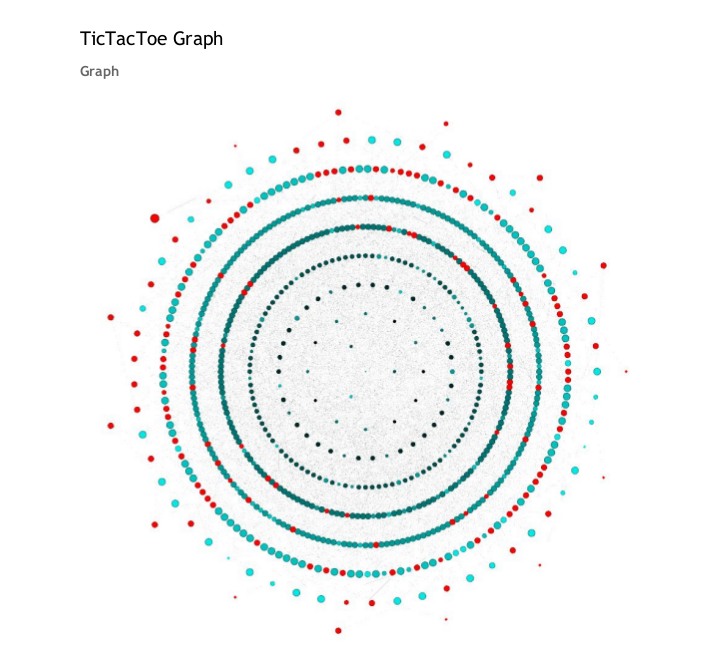
|
Jonathan Klawitter (Karlsruhe Institute of Technology)

|
Kaiwen Liang (University of Sydney)
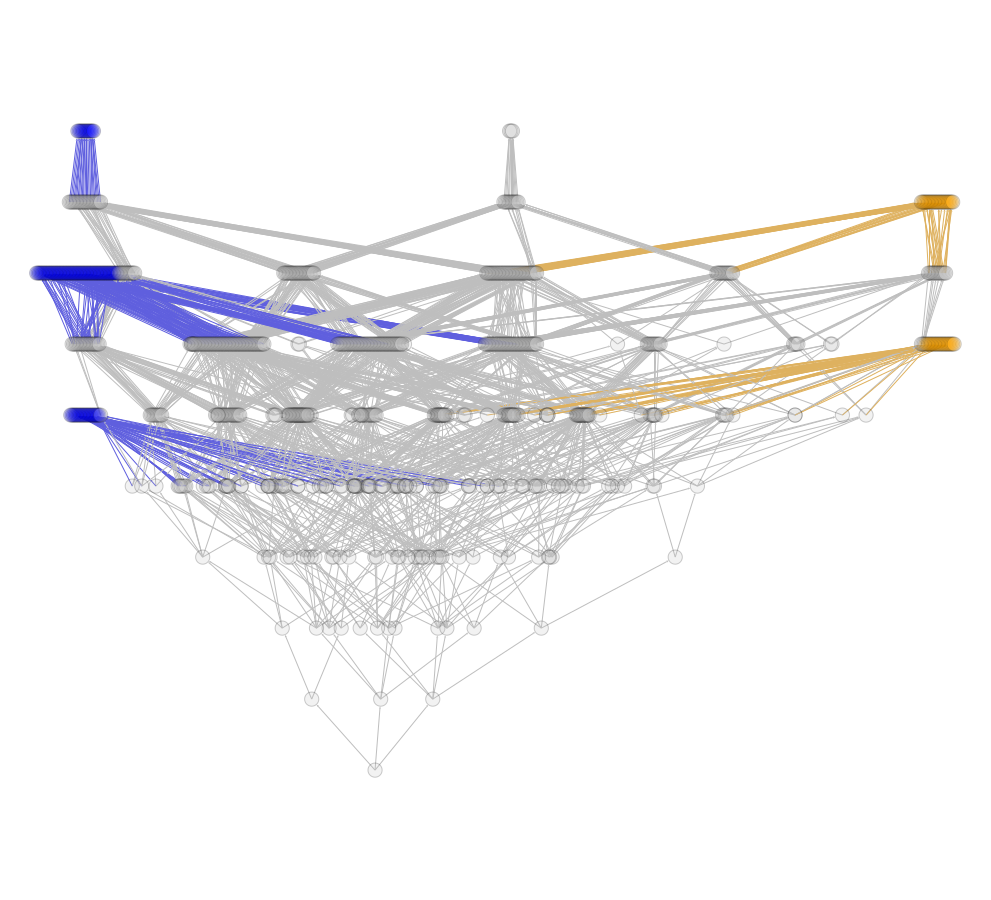
|
Kuok Cheng Tang (University of Sydney)

|
Then, we present two runners-up. These drawings were selected for the top three and displayed on large poster boards at the symposium.
Remus Zelina, Sebastian Bota, Siebren Houtman, and Radu Balaban (Meurs)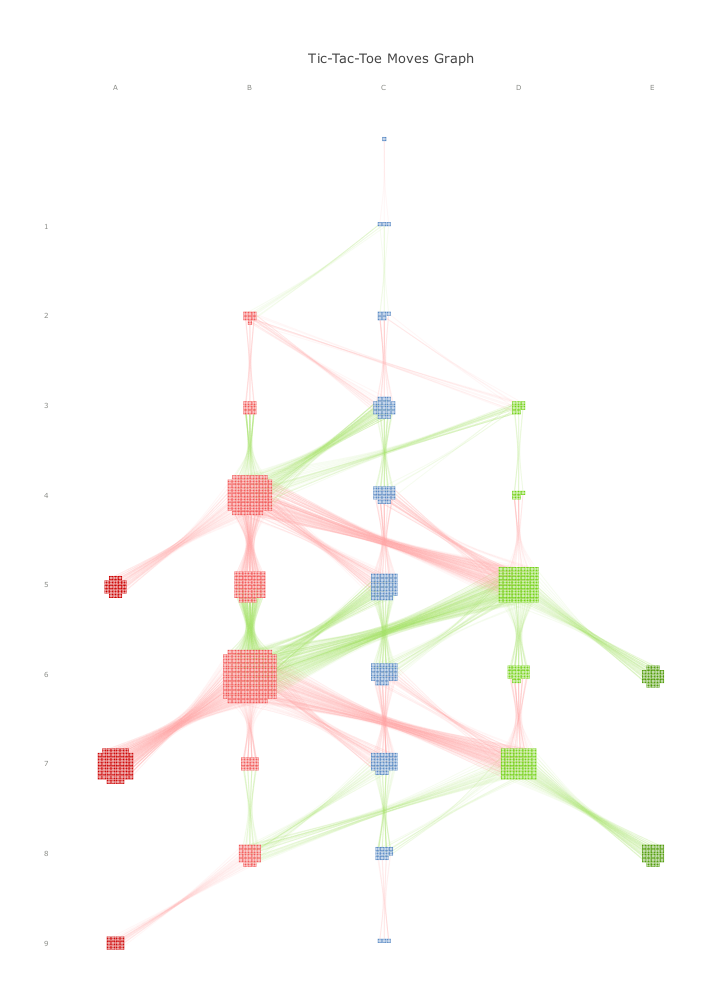
The committee really liked visual appeal of the full drawing, which clusters the individual node into groups based on the ply (number of moves played) and the current winner after optimal play. This way, the drawing clearly shows a much smaller meta-graph (25 nodes and 39 edges), with colours encoding game state and "size" of clusters encoding the number of actual board positions that belong to that state, that nicely communicates the global structure of the game.
Evmorfia Argyriou, Michael Baur, Anne Eberle, and Martin Siebenhaller (yWorks)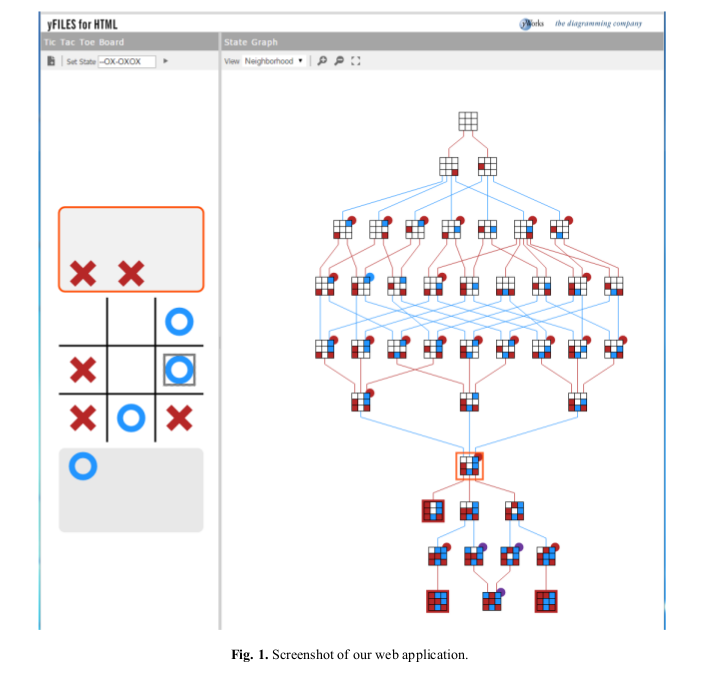 live.yworks.com/gd2015-contest/TicTacToe
live.yworks.com/gd2015-contest/TicTacToe
The committee liked the idea of using an interactive tool to explore the state graph. Using the tool, you can really see the impact of each move, making it very useful for understanding the game. The tool will dynamically show the local neighourhood (all possible paths to get to the situation, and all possible continuations) for any board position. Using small coloured disks, the winner after optimal play is visualised for individual nodes.
Finally, we announce the winner of the 2015 Graph Drawing Contest, Creative Topics: Tic-Tac-Toe:
Jennifer Hood and Pat Morin (Carleton University)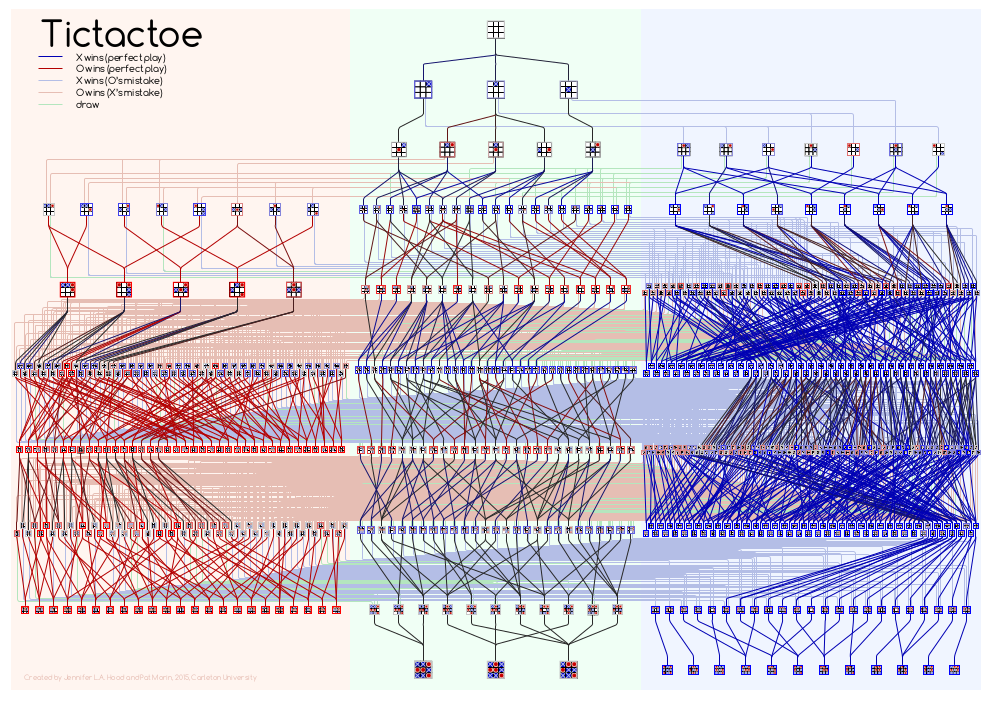
The committee was impressed by the way this drawing manages to illustrate the global structure of the graph, while still making it possible to follow individual paths and board positions. The global structure is nicely visualised by presenting the nodes in three columns, indicating which player will win upon optimal play, and nine rows, indicating the ply of the positions. Edge colours distinguish between move types (optimal or non-optimal, which player made the move, and which player wins). The committee especially liked the use of variable node sizes, making them small where necessary without affecting other parts of the drawing. Similarly, the committee liked the use of solid edges for the (relatively) small set of optimal-play edges and more faded colours for the non-optimal-play edges. Presenting the optimal-play edges (straight) in a different style than the non-optimal-play edges (orthogonal) further enhances their visual distiction.
Live Challenge: Manual Category
In the manual category, participants were presented with five graphs. We present the input layouts and the best manual submitted solutions.
|

|
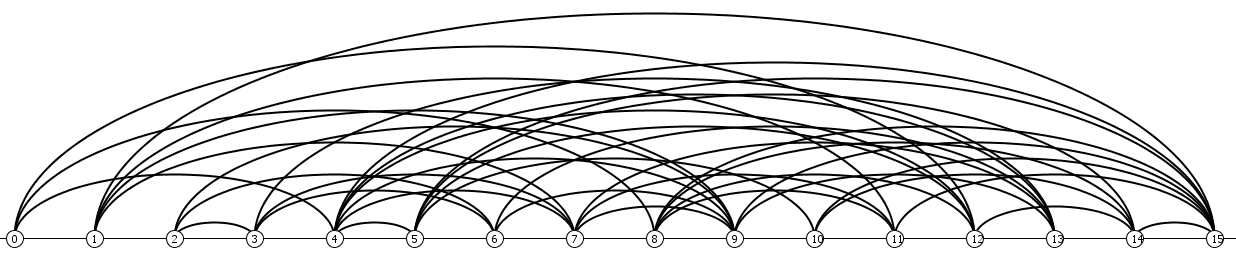
|
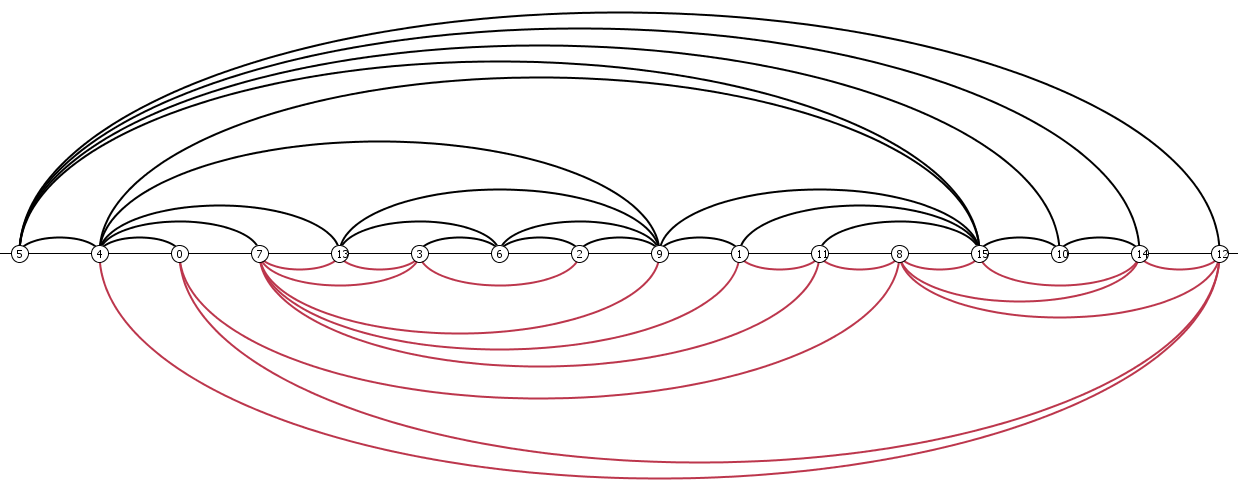
|
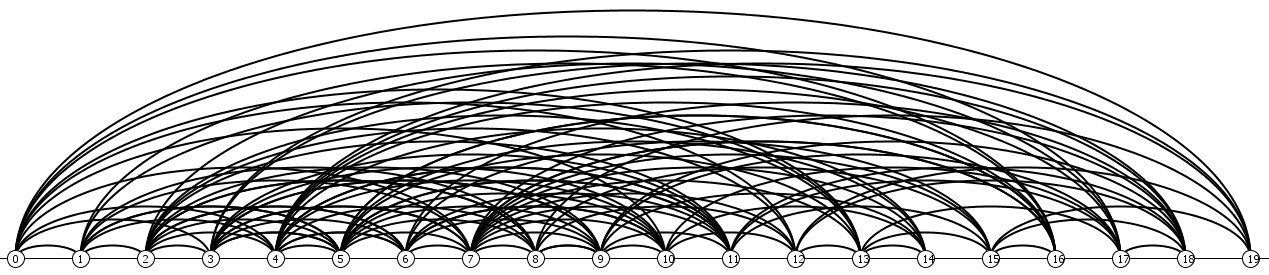
|

|

|
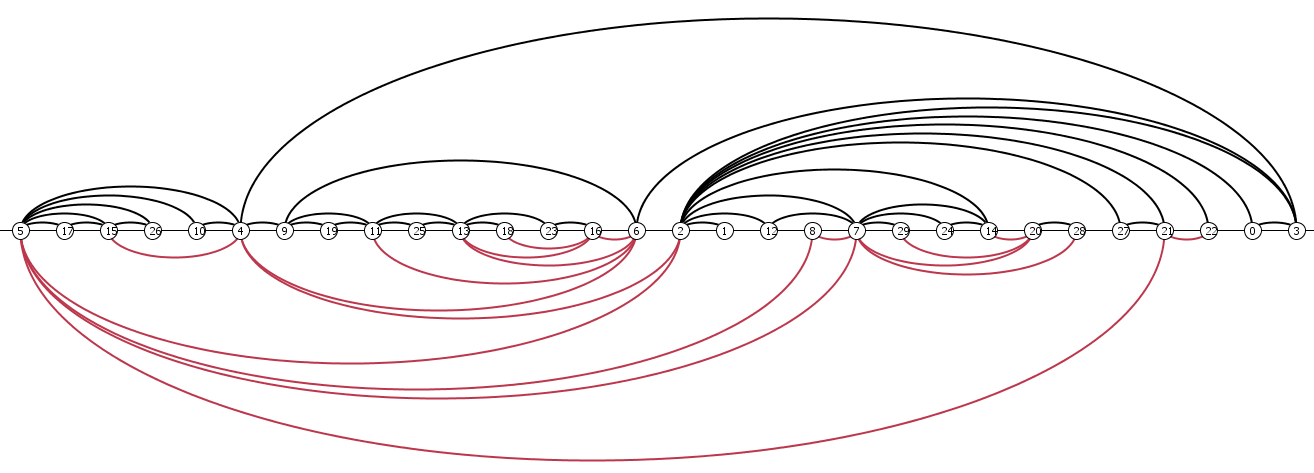
|

|

|
We are happy to present the full list of scores for all teams. The numbers listed are the number of crossings in each graph; the horizontal bars visualise the corresponding scores.
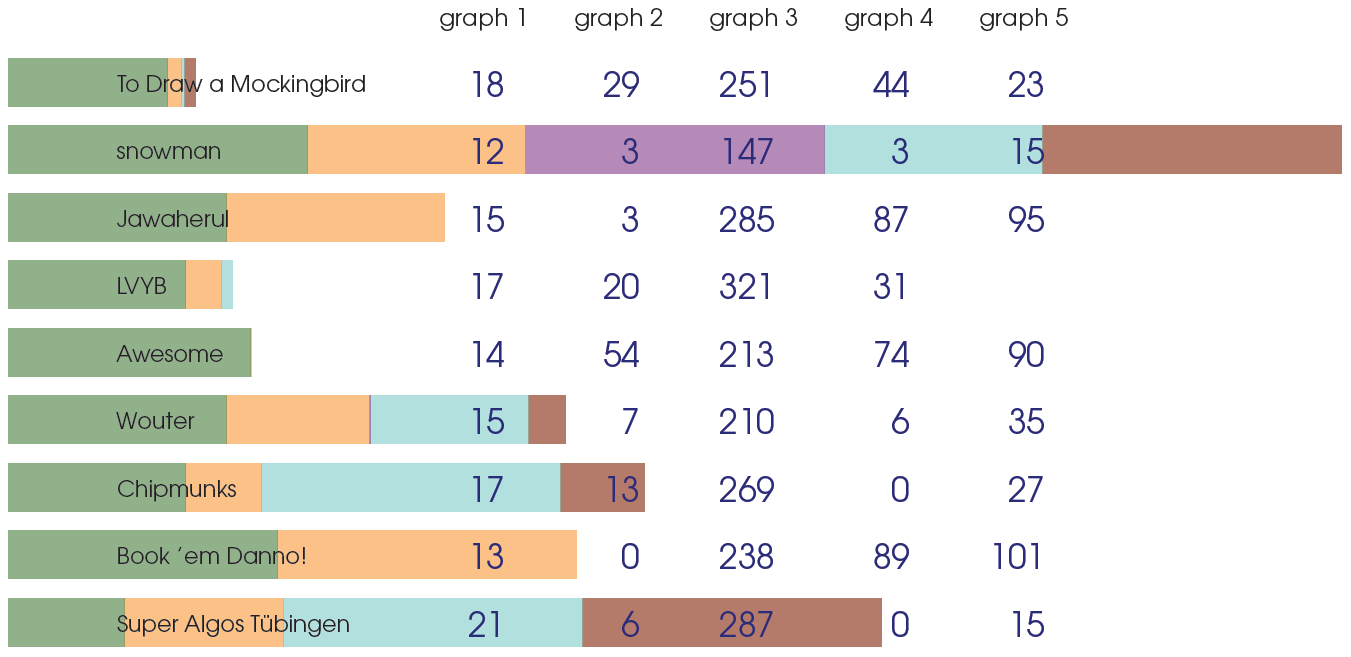
The winning team is team snowman, consisting of Boris Klemz, Ulf Rüegg, and Fabian Lipp!
Live Challenge: Automatic Category
In the automatic category, the same five graphs as in the manual category had to be solved, and in addition another set of five much larger graphs. The larger graphs are too large to visualise, so we present only a table of the best solutions.
Again, we are happy to present the full list of scores for all teams. The numbers listed are the number of crossings in each graph; the horizontal bars visualise the corresponding scores.

The winning team is team pepa, consisting of Josef Cibulka!
