Graph Drawing Challenge (Upward Crossing Reduction)

As with last year's contest, we shall hold the Graph Drawing Challenge in a format similar to a typical programming contest. At the start of the challenge, teams of contestants will receive the collection of challenge-graphs. After one hour, the teams will submit their final drawings and the team with the highest cumulative score wins.

Teams will be allowed to use any combination of software and human interaction systems to produce the best drawings. To accommodate both teams wishing to prepare for the challenge and teams wishing simply to participate, with no preparation, we will be providing, in advance, a small set of graph visualization tools. These tools are not necessarily meant to solve the problems at hand but are there to help the teams manually draw and manipulate the graphs. To further the development of new tools and to help promote tools already in existence, teams are also welcome and highly encouraged to create and bring their own software packages.

There exist two categories in the challenge that are judged differently:

• Automatic - This category is for teams using their own tool. Since we assume that the tool contains special algorithms to solve the challenge automatically, these teams will receive larger challenge graphs. Manual fine-tuning is allowed.
• Manual - This category is for teams using the provided graph editor. The graph editor does not contain any specific algorithm to solve the challenge. It allows only to move nodes and to re-route edges. This category is for creating manual solutions without help of an automatic algorithm. Teams in this category will receive smaller challenge graphs.

This year the challenge focuses on minimizing the number of crossings of upward grid drawings of graphs with edge bends. The challenge graphs will be directed, acyclic and non-planar. Multiple edges between the same pair of nodes may occur. In particular, all drawings must have the following properties:

• All nodes are placed on distinct integer grid locations.
• Edges can have bends. All bends are placed on distinct integer grid locations.
• Edges start at the source node and end at the target node. Due to the bends, they form a path of edge segments from the source to the target node.
• All edge segments must be upward; i.e., the start point of the segment must have a strictly smaller y-coordinate than the end point of the segment. There is no restriction on the x-coordinate.
• Node and edge overlaps are forbidden.
• Use the smallest number of edge crossings.

The results are judged solely with respect to the number of edge crossings. Other aesthetic criteria such as symmetry of the placement or use of area are not taken into account. This allows an objective way to qualitatively evaluate a given drawing. With this challenge, we hope to attract (not exclusively) all teams that have developed an automatic Sugiyama-style layout or any alternative approach for directed acyclic graphs.

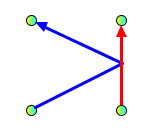
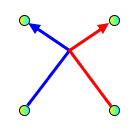
Here are some examples of allowed and forbidden situations. For the challenge, it does not matter whether the y-axis is oriented in mathematical convention with increasing coordinates towards the top, or in English reading direction with increasing coordinates towards the bottom, but in the drawings below, the origin (0,0) is near the bottom left corner, that is, the y-axis is drawn in mathematical convention.

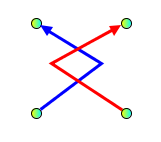
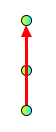
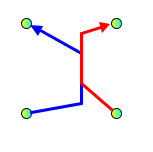
Allowed: 2 crossings	Forbidden: Node overlaps edge	Forbidden: Edge segments overlap	Forbidden: Edge bend on other segment	Forbidden: Knockknee (bends on same location)

Here is an overview of the rules for the challenge:

• The challenge will take place for one hour during the Graph Drawing Symposium.
• Teams may consist of one to three participants each. Each team may bring their own computers and/or software tools to the challenge.
• Software tools for manually solving the challenge will be provided for each team with time available prior to the challenge to set-up and practice with the system.
• At the start of the challenge, contestants will receive a collection of five to ten graphs. The graphs will be directed acyclic non-planar with twenty to five thousand nodes.
• For each graph, the team submitting the drawing with the smallest number of crossings receives the highest score. Scores for other submissions of the same graph shall be weighed with respect to this value. The team with the highest total score over all graphs wins.

Remote Participation

For those teams that cannot attend the conference but still wish to compete (in the automatic category), we allow remote participation. A few key points:

• Participants should contact the committee prior to the contest, and preferably as early as possible, to help determine the number of remote teams and to coordinate the instructions.
• At the time of the challenge, remote teams will be able to access an online location (website) to download the data sets and then simply submit the results via email.
• Detailed submission instructions will be provided on this site at a later time.

Graph Format

For the GD2008 contest, a modified ASCII format described below will be used. The contest graphs will be provided in this format and the final submissions should be prepared using the same format.

• The first number (N) indicates the number of nodes in the graph.
• The next 2N numbers contain the coordinates of the nodes. Each coordinate consists of the x and the y value of the node, indicating its position.
• The remainder of the file contains the edges. For each edge, the first value is the index of the source node, and the second value is the index of the target node. Next follows an array with an even number of values, enclosed by [ ... ], which are the x and y coordinates of the bend points of the edge.
• An edge that has no bend points is written as an empty bend array [].
• The nodes are labeled from 0 to N-1 and the order from the input file must be used in the output file as well.
• Comments are allowed as indicated below.
• The edge order is not important.
• The contest graphs will have random start locations for the nodes.
• All numbers are integers.

Sample File

Below is a simple example:

# Lines starting with # are comments and ignored
# First value is NumNodes(N)
5
#
# Next N pairs are x and y coordinate values of each node
10 0 # Node 0
5 5  # Node 1
0 10 # Node 2
0 8  # Node 3
10 2 # Node 4
#
# Remaining lines are the edges.
# The first value is the source node.
# The second value is the target node.
# The values between [ ... ] are grouped in pairs as bend points (X,Y) 
0 2 [ 9 5 5 9 ] # Edge from Node 0 to Node 2 with bend points (9,5) and (5,9)
0 4 []          # Edge from Node 0 to Node 4 with no bend points
0 1 []          # Edge from Node 0 to Node 1 with no bend points
0 3 [ 0 1 ]     # Edge from Node 0 to Node 3 with bend point (0,1)
4 1 []          # Edge from Node 4 to Node 1 with no bend points
4 3 [ 5 4 ]     # Edge from Node 4 to Node 3 with bend point (5,4)
4 2 [ 10 9 ]    # Edge from Node 4 to Node 2 with bend point (10,9)
1 3 []          # Edge from Node 1 to Node 3 with no bend points
1 2 []          # Edge from Node 1 to Node 2 with no bend points
3 2 []          # Edge from Node 3 to Node 2 with no bend points

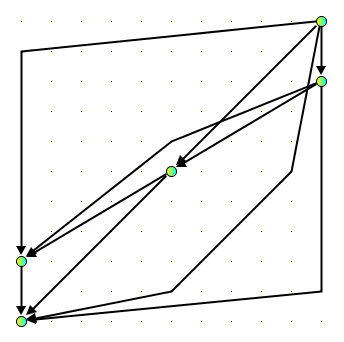
The diagram below corresponds to this input file. It displays the K5 in a legal upward layout, however the number of crossings in this layout is not optimal. In this picture, the origin (0, 0) is near the top left corner (English reading direction). If your software has the origin at the bottom left corner (mathematical convention), your image will be mirrored in y direction.

Legal notice